
Para recolectar dinero, hace 80 días, un
grupo de estudiantes de la USIL ha venido
recogiendo botellas usadas que planea
llevar a una empresa dedicada al reciclaje
de vidrios. A la fecha han recolectado 24
000 kilogramos de vidrio por las cuales la
empresa de reciclaje ofrece S/ 0,20 por
kilogramo. Sin embargo, como las botellas
se están acumulando con más rapidez que
las que se pueden reciclar, la empresa
planea reducir 1 céntimo cada día el
precio que pagará por 100 kilogramos de
vidrio usado. Suponga que el grupo de estudiantes puede continuar recolectando botellas a la misma tasa y que los costos de transporte no permiten realizar más de un viaje al local de la empresa recicladora de vidrios. Según esto:
a) Modele la expresión matemática para el ingreso del grupo de estudiantes proveniente de su proyecto de reciclaje como una función del número de días adicionales que durará su proyecto.
a) Primer paso: Analizamos los datos
En 80 días, se recolectaron 24000 kg de botellas de vidrio. Como el grupo de
estudiantes recolecta a la misma tasa entonces, en 1 día, se recolectan 300kg de
botellas.
Si la empresa ofrece S/0.2 por kilogramo, entonces en un día recaudan 60 soles. Sin
embargo, como sabemos que después descontarán S/0.01 por día cada 100 kg,
diremos que los estudiantes recaudan S/20 cada 100kg.
Por lo tanto,
Segundo paso: Ingresos por día
Día 1: 3(20) soles
Día 2: 2(3)(20) soles
Día 3: 3(3)(20) soles
Día 4: 4(3)(20) soles
Día 80: 80(3)(20)
A partir de aquí, se comienza a descontar S/0.01 por día
Día 81: (81)(3)(20) -0.01
Día 82 : (82)(3)(20) – (2)(0.01)
De tal forma que,
Donde n es la cantidad de días que pasan luego de 80 días.
Tercer paso: Ingreso en función del número de días adicionales que durará el proyecto.
El ingreso se calcula de la siguiente manera:
Donde x: 80 + n , y, por lo tanto, n: x-80.
También sabemos que,
x>80, ya que son los días adicionales y,
y>0, caso contrario no habría ingresos.
b) Use algún software para graficar la función obtenida en el ítem anterior.
c) ¿Es continua la función? De tener discontinuidades, identifique el tipo justificando analíticamente su respuesta.
La función I(x) es continua en todo su dominio ]80, 2140] ya que no presenta ninguna discontinuidad.
d) Determine cuando debería concluir el grupo de estudiantes su proyecto de venta de botellas con el fin de maximizar su ingreso. Justifique sus resultados con la derivada.
Para optimizar la función utilizamos el criterio de la segunda derivada, sin embargo, en este caso podemos resolverlo haciendo
solamente uso de la segunda derivada y encontrando su extremo máximo.
Primer paso: Encontramos I'(X).
Segundo paso: Igualamos I'(X) a 0 para encontrar el punto crítico.
Tercer paso: Armamos tabla para evaluar el punto crítico.
Rta: Los estudiantes deberían concluir su proyecto en el día 1040 ya que obtendrían un ingreso máximo de S/32448.

SITUACIÓN PROBLEMÁTICA 1

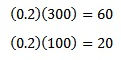





SITUACIÓN PROBLEMÁTICA 2

El impuesto sobre el carbono es
un impuesto medioambiental sobre la
emisión de dióxido de carbono, gas de
efecto invernadero, que pretende limitar
su uso. Este impuesto desalienta las
emisiones de contaminantes, haciendo
pagar a los contaminadores en
proporción a sus emisiones.
En la gráfica adjunta se muestra la relación entre los distintos niveles de impuestos al carbono y el porcentaje de reducción emisiones de CO2.

a) ¿Qué tasa de impuesto se tendría que imponer para lograr una reducción mundial del 50% en emisiones de CO2.?
Sabemos que el dominio de la función es [0,500]. También, al mirar la gráfica podemos ver que el vértice de la función está en (500,100). Por lo tanto, con estos valores ya podemos armar la función de la gráfica. Según la ecuación de la función cuadrática,
Reemplazamos,
Ahora, para encontrar a reemplazamos en un punto cualquiera. Elegimos el punto (0,0)
Por lo tanto,

Obtenemos una reducción mundial del 50% en emisiones de CO2 cuando y=50. De tal forma que,
Resolviendo queda que,
Sin embargo, no tomamos en cuenta ya que este valor no pertenece al dominio de la función. Entonces,
Rta: La tasa de impuestos que se tendría que imponer para lograr una reducción del 50% en las emisiones de CO2 es de $146,44.
b) Use la gráfica para calcular la razón de cambio de la reducción porcentual en emisiones de CO2.cuando la tasa de impuesto es de $200 por TM.
a razón de cambio cuando la tasa de impuesto es de $200 es f’ (200).
Para obtener el valor debemos obtener la pendiente de la recta tangente que pasa por el punto (200, f(200)).
Por lo tanto, nuestro primer paso será encontrar f’(x).
Ahora, reemplazamos cuando x=200.
Rta: La razón de cambio de la reducción porcentual en emisiones de CO2 cuando la tasa de impuesto es de $200 por TM es de 0,24%.




